本文要点：

· “谐波失真”通常表示在时域中观察到的波形失真。
· 谐波失真可从功率谱或时域波形中观察到，有多种表现形式。
· 不同形式的非线性会产生不同类型的谐波失真。

任何模拟信号只要存在一定程度的非线性，都会产生谐波失真。模拟信号失真时，信号在时域中的外观会发生变化，表现为波形压缩或完全偏移。谐波模拟信号中的谐波失真已是老生常谈，但调制信号或方波/锯齿波中也明显存在各类谐波失真，其中一个常见的例子是功率放大器，它们在运行时通常接近饱和点。

谐波失真对信号的影响取决于产生失真的元件，甚至是信号的测量方式。那么问题来了，如何厘清信号中谐波失真的类型？有没有方法直接测量或计算？本文将举例介绍不同类型的谐波失真，以及产生的原因。

谐波失真类型

一般来说，通过观察波形，可以发现五种类型的谐波失真：

1. 振幅失真
2. 频率失真
3. 相位失真
4. 互调失真
5. 交叉失真

除了非线性产生的非线性失真外，上述类型的谐波失真只出现在宽带信号或离散频率相加的信号上。

1. 振幅失真与频率失真

这两个术语有时会互相替代，但一般所指并非同类。二者在时域上看似相似，但在频域上却完全不同。在时域测量中，振幅失真与频率失真区别如下：

振幅失真：当电路或设备产生的输出信号的幅值是输入幅值的非线性函数时，就会出现这种情况。振幅失真是由非线性引起的，可以在谐波信号或宽带信号中观察到。这种现象有时被称为削波失真，因为它发生在饱和器件（如放大器）中。

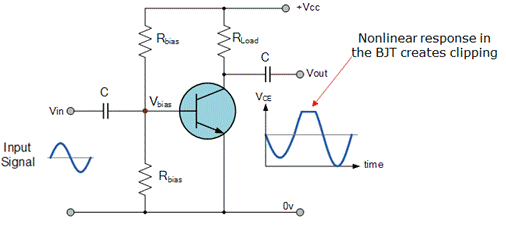
由于饱和，振幅失真通常表现为削波

频率失真：当电路或设备导致输入信号中不同频率器件的电压/电流发生不同程度的变化时，就会出现频率失真。频率失真只能在宽带信号中观察到。当伯德图的幅值为非线性时，滤波器通常会出现频率失真。

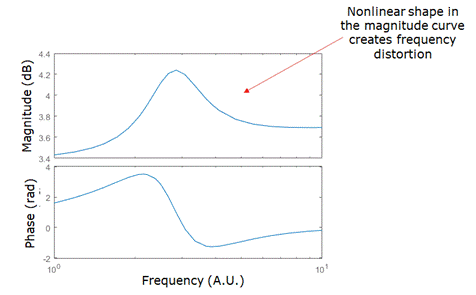
伯德图中幅值曲线的形状会导致宽带信号中出现频率失真

在实际器件中，振幅失真可能只在特定频率范围内产生；为了加以区分，这种现象可称为“非线性频率失真”，此时还应该说明非线性在实际器件和电路中的重要性。

2. 相位失真

当滤波器的传递函数（伯德图）的相位是频率的非线性函数时，滤波器就会产生相位失真。此时输出波形会出现失真，但不一定是因为波形出现了削波或其他幅值效应，而是因为群速度和相速度不是恒定值，因此组成信号的不同频率会以不同的速度传播。

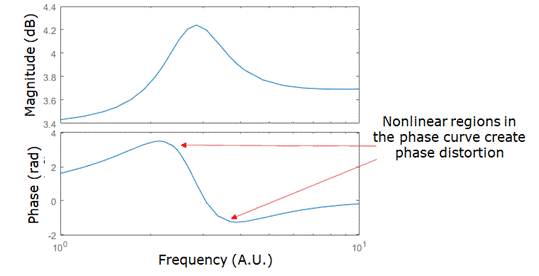
伯德图相位曲线中的非线性区域会因色散而产生相位失真

3. 互调失真

当频率调制信号或其他宽带信号馈入非线性器件时，会出现互调失真。具体来讲，当输入接近饱和状态时，互调失真就会常见于功率放大器，此时，构成输入信号的离散频率相加会产生和/差谐波。

最突出的一组和/差谐波是三阶互调。这些谐波最有可能出现在放大器的线性输入区，且最接近输入信号功率谱的频带边缘。在时域中，互调失真表现为频率略高于输入信号载波频率的低振幅噪声。

4. 交叉失真

在推挽式晶体管放大器中，特别是在使用三极管（Bipolar Junction Transistor，BJT）的放大器中，信号可能会出现交叉失真。当一对晶体管中有一个进入截止区时，输出信号会短暂降至零，此时就会发生交叉失真。实际上，当输入信号处于低电平时，放大器中的两个晶体管都没有开启，因此即使输入信号不为零，输出信号也为零。下面是一个简单的时域示例。

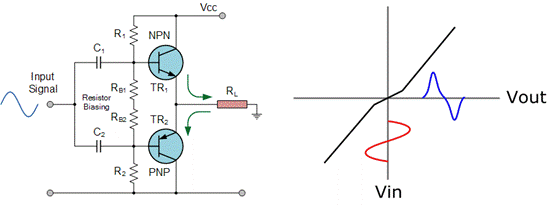
推挽（B 类）放大器中的交叉失真

如何发现谐波失真

在测量或仿真中很容易发现上述类型的谐波失真：只需比较相关器件或电路的输入和输出信号即可。如果两者在时域和频域上不是线性函数关系，则说明存在某种失真。在设计阶段，仿真工具可以让电路中可能出现的谐波失真问题无处遁形。

在设计低失真的真实器件系统时，Cadence 的系统分析工具集可以帮助设计人员发现信号中的各类谐波失真，从而采取有效措施。

PSpice 仿真工具可用于生成所需的仿真，识别和优化低谐波失真电路，并利用内置建模应用对实际电路进行仿真。